Range shift by stochastic long distance dispersal
On the last day of the workshop "Climate change and its implications for ecosystem dynamics and functioning", the group "ecosystem boundaries" was discussing whether it is absolutely necessary for shifting the range of a species that its outposts have gene flow with the core population (prompted by the talk of Jutta Buschbom) or is the fundamental process just the result of stochastic long-distance dispersal and extreme events during establishment and at time of death. On the way home I constructed a small model to answer the question. It seems that stochasticity is sufficient and no preadaptation is necessary if long distance-dispersal is faster than climate change (an unexpected support for climate envelope models). A second question was whether the variability within the species would decrease if there is no gene flow. I haven't tested this yet but have ideas how to implement that. I am sending you the source code for "R" so you can play with it. If you don't have R you can at least look at the movie. More details on the model are in the source code. I have not checked whether this is new for science, but if you think it is and want to explore the issue further, let me know.
Source code
##############################################################################################
# A simulation for testing the assumption that plant populations can migrate with
# the changing climate by long distance dispersal, establishing outposts, but
# without having genetic exchange with the core population. The central issue is:
# is genetic exchange absolutely necessary or can populations persist without. The
# question came up during a discussion at the ZIF Workshop on climate change
# impacts on ecosystem functions and processes in temperate and boreal ecosystems,
# Bielefeld, August 2008. This program was designed on the way home (and the night
# after) and to be as simple as possible.
#
# MODEL SETUP
# The model divides a region (e.g. a continent) into discrete grid cells. A
# climatic gradient (e.g. mean annual temperature) decreases from South to North
# across the grid. A second climatic gradient (e.g. mean annual precipitation)
# decreases from West to East. This second gradient does not change in this
# version and does not affect the result. I introduced it to get a circular range
# for the species instead of a less intuitive band.
#
# RULES of the simulation:
# An individual can either be alive (cell state 1) or be dead (cell state 0). All
# individuals are identical. That means they have the same response to the
# climatic factors.
#
# The primary climate gradient increases by a fixed value per time step all over
# the region. (Fixed annual increase of mean annual temperature by x°C.)
#
# In each time step a live individual can disperse seeds into empty cells.
# The dispersal function is negative exponential. Here one could implement more
# appropriate functions that result in more frequent long-distance dispersal.
# Each individual disperses one seed into an arbitrary direction. The issue is
# long-distance dispersal, therefore concentrating on one seed is approriate.
#
# The climate at time of establishment is assumed to be the most critical
# criterion for estblishment. This could be late frosts, minimum germination
# temperature, or something else. The point is that this is an extreme event whose
# probability is nonetheless tied to the mean annual climatic value. This is no
# absolute requirement and could be changed in more complex versions of the model.
# In this version, the climate at time of establishment is thought of as the mean
# annual temperature minus a fixed value (delta.lo) plus some normally distributed
# variation for simulating extreme events. The normal distribution should be
# replaced by a more appropriate distribution for extreme events.
#
# Similar to the climate at time of establishment, climate extremes may also cause
# the death of individuals (e.g. heat stress in summer, drought, pests). The point
# here, too, is that this is an extreme event somehow tied to the mean annual
# value. In this version, the climate at time of death is thought of as the mean
# annual temperature plus a fixed value (delta.hi) plus some normally distributed
# variation for simulating extreme events. As before, the normal distribution
# should be replaced by a more appropriate distribution for extreme events.
#
# Other factors than climate cause the death of individuals. These are simulated
# by random mortality with a poisson distribution and limits set by the second
# climatic gradient (with normal variability) in each time step.
#
#
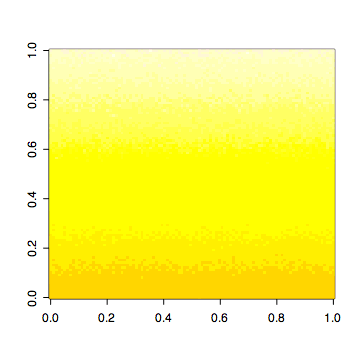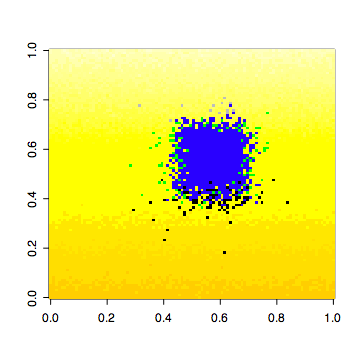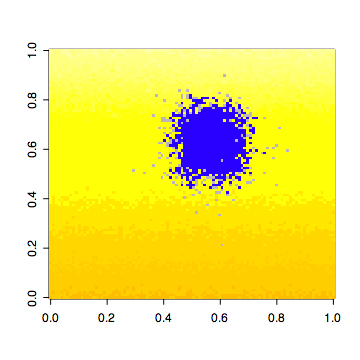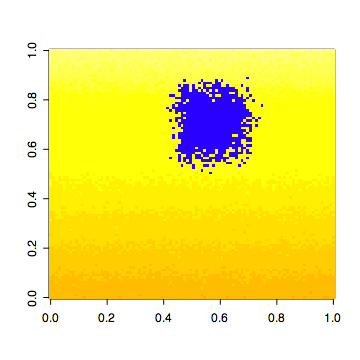
# LEGEND
# yellow-red: the primary climate gradient
# blue: live individuals
# gray: seeds dispersed in the current time step
# green: individuals established in the current time step
# black: individuals killed in the current time step
#
# EXPERIMENTS
# Decrease the dispersal distance or increase the change of climate
# Change the variability of the climate gradient
# Increase the speed of climate change
#
# VERSION 1.0 Martin Köchy 2008-09-03
# uniform population
# VERSION 2.0 Martin Köchy 2008-09-11
# diverse population
############################################################################################
Nmax=100 # length of the edge of the landscape, number of cells
estab=5 # climatic criterion for establishment of an individual
kill =35 # climatic criterion for the death of an individual
delta.lo = 5 # climate at time of establishment, difference to mean annual value
delta.hi = 10 # climate at time of death, difference to mean annual value
R.grow.lo = 300 # lower limit of second limiting environmental criterion for survival
R.grow.hi = 500 # upper limit of second limiting environmental criterion for survival
CC.step=0.5 # Fixed overall change in the primary climatic gradient
n.steps = 20 # number of time steps to simulate, use between 10 and 50
mean.dispersal.distance = 5 # a parameter for the dispersal function (in cell units)
spring.var.sd = 1 # standard deviation of the climate criterion at time of establishment
summer.var.sd = 1 # standard deviation of the climate criterion at time of death
mort.rate = 0.01 # mean mortality rate by random events independent of climate (Poisson
# distribution)
rain.var = 20 # stadard deviation of the second climatic criterion
T.range.display=250:(250-max(Nmax,50)) # colours for display of primary climatic gradient
# A function to restrict dispersed species to the grid
limit = function(f) {min(max(f, 1), Nmax)}
# Setting up the primary climate gradient, e.g. mean annual temperature
T = rep(seq(40,-5, length.out=Nmax), each=Nmax)
T.grid = matrix(rnorm(Nmax*Nmax, T, 1), nrow = Nmax)
# Setting up the secondary climate gradient, e.g. mean annual precipitation
R = rep(seq(800,100, length.out = Nmax), Nmax)
R.grid = matrix(rnorm(Nmax*Nmax, R , 20), nrow = Nmax)
# Display the first gradient
image(T.grid, col=rev(heat.colors(256)[T.range.display]))
# Setting the initial population within the species' climatic range
S.grid = matrix(floor(rlnorm(Nmax*Nmax, log(4), log(1.3))),nrow=Nmax, ncol=Nmax) # The grid for the individuals
S.grid = ifelse(T.grid>estab+delta.lo & T.grid < kill-delta.hi
& R.grid > R.grow.lo & R.grid < R.grow.hi,S.grid,0)
# Display the initial species distribution
richness = unique(as.vector(S.grid)[-1]) # number of species types
# The colours for live individuals
blueish=rgb(0, 10+seq(0, 10*richness, by=10), 255, maxColorValue=255)
image(S.grid, col=c(NA, blueish), add=TRUE)
# The simulation loop for each time step (e.g. a year)
for (n in 1:n.steps) {
# change the primary climate gradient
T.grid=T.grid+CC.step
# Setting up a temporary grid for dispersed seeds
S.grid.disp = matrix(0, ncol=Nmax, nrow=Nmax)
for (i in 1:Nmax) {
for (j in 1:Nmax) {
# Only live individual can disperse seeds
if (S.grid[i,j]>0) {
# each individual disperses one seed into an arbitrary direction
# and a random distance (here following a negative exponential function
dx = round(rexp(1,1/mean.dispersal.distance))*runif(1,-1,1)
dy = round(rexp(1,1/mean.dispersal.distance))*runif(1,-1,1)
# add the distances to the cell coordinates
idx = limit(i+dx)
jdy = limit(j+dy)
# update the grid
S.grid.disp[idx, jdy] = ifelse(S.grid[idx, jdy]==0, S.grid[i,j], 0)
}
}
}
# Show dispersed seeds in gray
image(S.grid.disp, col=c(NA, "gray"), add=TRUE)
# Set up a temporary grid for the climatic variation at time of establishment
spring.var.grid = matrix(rnorm(Nmax*Nmax, 0 , spring.var.sd), nrow = Nmax)
# Setting the climatic conditions at time of establishment
estab.climate.grid = T.grid - delta.lo + spring.var.grid
# Test whether climatic conditions are fit for establishment
S.grid.estab = ifelse(estab.climate.grid > estab & S.grid.disp, S.grid.disp, 0)
# Display the result
image(S.grid.estab, col=c(NA, "green"), add=TRUE)
# Update the grid containing individuals
S.grid = ifelse(S.grid.estab>0, S.grid.estab, S.grid)
# Set up a temporary grid for the climatic variation at time of death
summer.var.grid = matrix(rnorm(Nmax*Nmax, 0, summer.var.sd), nrow = Nmax)
# Setting the conditions at time of death
death.climate.grid = T.grid+delta.hi+summer.var.grid
# Test whether climatic conditions are mortal
S.grid.dead = ifelse(death.climate.grid > kill & S.grid, 1, 0)
# Display the result
image(S.grid.dead, col=c(NA, "black"), add=TRUE)
# Update the grid containing individuals
S.grid = ifelse(S.grid.dead, 0, S.grid)
# Random mortality independent of primary climate gradient
S.grid.dead = S.grid.dead * matrix(rpois(Nmax*Nmax, mort.rate), nrow = Nmax)
# Set up a temporary grid for the variation of the second climate gradient
R.grid = matrix(rnorm(Nmax*Nmax, R , rain.var), nrow = Nmax)
# Test whether secondary climate conditions are mortal and combine with previous condition
S.grid.dead = ifelse((R.grid < R.grow.lo | R.grid > R.grow.hi) & S.grid, 1, S.grid.dead)
# Display the result
image(S.grid.dead, col=c(NA, "black"), add=TRUE)
# Update the grid containing individuals
S.grid = ifelse(S.grid.dead==1, 0, S.grid)
# Update the colours for displaying the primary climate
T.range.display = T.range.display-1
T.grid.display = ifelse(S.grid>0,NA,T.grid) # exclude occupied cells (for speed)
# Display the updated result for the time step
image(T.grid.display, col=heat.colors(256)[T.range.display], add=TRUE)
image(S.grid, col=c(NA, blueish), add=TRUE)
}